Доверительный интервал и доверительная вероятность являются ключевыми понятиями математической статистики, используемыми для оценки точности результатов исследований и измерений. Эти инструменты позволяют количественно выразить неопределенность статистических оценок.
Содержание
Доверительный интервал и доверительная вероятность являются ключевыми понятиями математической статистики, используемыми для оценки точности результатов исследований и измерений. Эти инструменты позволяют количественно выразить неопределенность статистических оценок.
Основные определения
| Термин | Определение |
| Доверительный интервал | Диапазон значений, который с заданной вероятностью содержит истинный параметр генеральной совокупности |
| Доверительная вероятность | Вероятность того, что доверительный интервал действительно содержит оцениваемый параметр |
Характеристики доверительного интервала
- Границы интервала - нижняя и верхняя оценки параметра
- Ширина интервала - зависит от объема выборки и изменчивости данных
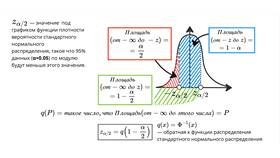
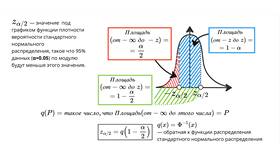
- Уровень значимости - вероятность ошибки (α = 1 - доверительная вероятность)
- Точность оценки - обратно пропорциональна ширине интервала
Как рассчитывается доверительный интервал
- Определение доверительной вероятности (обычно 90%, 95% или 99%)
- Вычисление точечной оценки параметра (среднее, доля и т.д.)
- Определение стандартной ошибки оценки
- Нахождение критического значения распределения
- Расчет границ интервала
Пример расчета для среднего значения
| Параметр | Формула |
| Доверительный интервал | x̄ ± t*(s/√n) |
| Обозначения | x̄ - выборочное среднее, t - критическое значение, s - стандартное отклонение, n - объем выборки |
Факторы, влияющие на доверительный интервал
- Объем выборки (чем больше n, тем уже интервал)
- Изменчивость данных (чем больше разброс, тем шире интервал)
- Выбранный уровень доверительной вероятности
- Тип распределения данных
Распространенные уровни доверительной вероятности
| Вероятность | Уровень значимости | Типичное применение |
| 90% | 0.10 | Предварительные исследования |
| 95% | 0.05 | Большинство научных работ |
| 99% | 0.01 | Высоконадежные оценки |
Интерпретация доверительного интервала
Правильное понимание результатов:
- Доверительный интервал относится к параметру генеральной совокупности
- 95% доверительная вероятность означает, что при многократном повторении исследования в 95% случаев интервал будет содержать истинное значение
- Широкий интервал указывает на большую неопределенность
- Если интервал включает нуль для разницы средних, эффект может отсутствовать
Доверительные интервалы и доверительная вероятность предоставляют более информативную альтернативу точечным оценкам, позволяя оценить точность статистических выводов и принять обоснованные решения в условиях неопределенности.
